Modelling the role of surface stress on the kinetics of tissue growth in confined geometries
Abstract
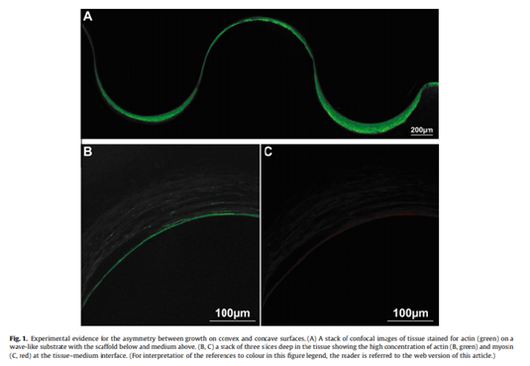
In a previous paper we presented a theoretical framework to describe tissue growth in confined geometries based on the work of Ambrosi and Guillou [Ambrosi D, Guillou A. Growth and dissipation in biological tissues. Cont Mech Thermodyn 2007;19:245–51]. A thermodynamically consistent eigenstrain rate for growth was derived using the concept of configurational forces and used to investigate growth in holes of cylindrical geometries. Tissue growing from concave surfaces can be described by a model based on this theory. However, an apparently asymmetric behaviour between growth from convex and concave surfaces has been observed experimentally, but is not predicted by this model. This contradiction is likely to be due to the presence of contractile tensile stresses produced by cells near the tissue surface. In this contribution we extend the model in order to couple tissue growth to the presence of a surface stress. This refined growth model is solved for two geometries, within a cylindrical hole and on the outer surface of a cylinder, thus demonstrating how surface stress may indeed inhibit growth on convex substrates.