Tissue growth controlled by geometric boundary conditions: a simple model recapitulating aspects of callus formation and bone healing
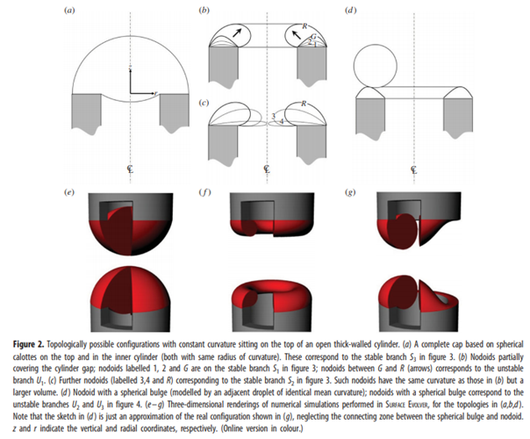
The shape of tissues arises from a subtle interplay between biochemical driving forces, leading to cell growth, division and extracellular matrix formation, and the physical constraints of the surrounding environment, giving rise to mechanical signals for the cells. Despite the inherent complexity of such systems, much can still be learnt by treating tissues that constantly remodel as simple fluids. In this approach, remodelling relaxes all internal stresses except for the pressure which is counterbalanced by the surface stress. Our model is used to investigate how wettable substrates influence the stability of tissue nodules. It turns out for a growing tissue nodule in free space, the model predicts only two states: either the tissue shrinks and disappears, or it keeps growing indefinitely. However, as soon as the tissue wets a substrate, stable equilibrium configurations become possible. Furthermore, by investigating more complex substrate geometries, such as tissue growing at the end of a hollow cylinder, we see features reminiscent of healing processes in long bones, such as the existence of a critical gap size above which healing does not occur. Despite its simplicity, the model may be useful in describing various aspects related to tissue growth, including biofilm formation and cancer metastases.